OPTIMUM PID CALCULATION
Reformulated Tangent Method ©

Abstract

This webpage will present an alternative method of analyzing open-loop response of a process.
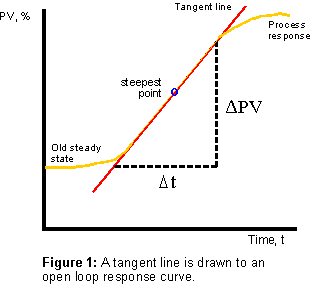
In the conventional tangentmethod, the process response rate is obtained by drawing  a tangent
line at the steepest point of the response curve and calculating  the response rate of the tangent
line. This analysis is normally performed on a chart paper or on a hard copy of a DCS. A  new
proposed technique transforms the process response rate calculation into a trigonometric function.
A protractorwill be used to measure the angle made between the base line of past steady-state
level and the tangent line. This technique simplify and reduce the steps in analyzing the process
response rate. Frequent analysis can be done faster and the analysis can be performed directly on
console as compared to the existing method.

Reformulation of Response Rate Calculation

In the tangent method, to calculate the optimum PID, a tangent line should be drawn at the
steepest point of a processresponse curve. The process response rate is the process
change per change in time as shown below.

Response rate is the slope of the open loop response curve. Therefore,

The response curve as in Figure 1 can be  analyzed  and  viewed with different perspective as
in  Figure 2.

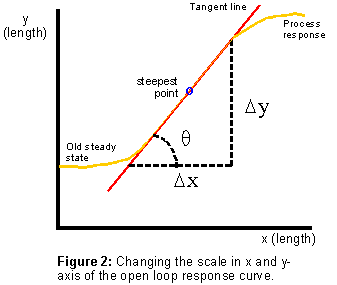
Then, the response rate would be,

     
Combining equation (i) and (ii) together,

But equation (iii) is not dimensionally correct. y and x have units of length; while, PV and t have
units of  % and time,respectively. Hence, a conversion factor must be added to the right hand
side of equation (iii).

     where,
                  (% / length) is the conversion factor of the response (PV) scale
                  (time / length) is the conversion factor of the time (t) scale

Finally, recognizing that y / x  = tan , equation (iv) transforms into

The right hand side of equation (v) provides an alternative means of analyzing process
response rate.

(Publication of this method in any journals, papers, magazines or conferences for personal
accreditation must obtain  a written permission from Abdul Aziz Ishak at aabi63@hotmail.com
or aabi63@kkps.fk.um.edu.my)

APPLICATION EXAMPLES